图示:
代码
#includeusing namespace std; struct node { int s; // 起点 int e; // 终点 int l; // 长度 }e[100]; int num[100]; bool cmp(node a, node b) { return a.l < b.l; } int getf(int v) // 查找v的根元素 { if(num[v] == v) // 如果自己是直接的根元素 return v; else { num[v] = getf(num[v]); // 用递归找到根元素 return num[v]; } } int add(int v, int u) // 合并函数 { int t1, t2; t1 = getf(v); // 找到v的根元素 t2 = getf(u); // 找到u的根元素 if(t1 != t2) // 如果v的根元素不等于u的根元素则置为相同 { num[t2] = t1; return 1; // 不连通返回1 } return 0; } int main() { int a, b; int n, m, cnt = 0, sum = 0; cin >> n >> m; for(int i = 1; i <= m; i++) // 输入m条边的数据 cin >> e[i].s >> e[i].e >> e[i].l; sort(e + 1, e + m + 1, cmp); // 将没一条边的权值(长度)进行从小到大排序 for(int i = 1; i <= n; i++) // 将自己置为自己的根元素 num[i] = i; for(int i = 1; i <= m; i++) { if(add(e[i].s, e[i].e)) // 判断2个点是否连通不连通则执行 { cnt++; sum += e[i].l; } if(cnt == n - 1) // 总共有m-1条边 break; } cout << sum << endl; }
输入:
6 9
2 4 11
3 5 13
4 6 3
5 6 4
2 3 6
4 5 7
1 2 1
3 4 9
1 3 2
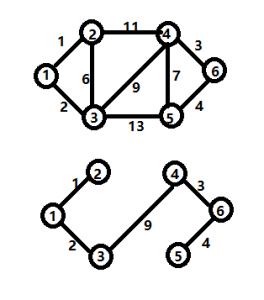
输出:
19
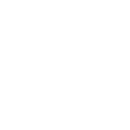


Comments | NOTHING